Retour à l'accueil principal
Convolution
 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
Accueil

Propriétés
Linéarité
Décalage en temps/fréquence
Dérivation
Dilatation en temps/fréquence
Conjugaison complexe
courantConvolution

Table des matières
Index
Définition : Soient deux signaux x et y à valeurs continues et à temps continu. On définit le produit de convolution des deux signaux, ou plus simplement leur convolution, par :
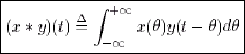Définition de la convolution(1.12)
On vérifie aisément que (x*y)(t)=(y*x)(t), c'est-à-dire que la convolution est commutative, par :
Commutativité de la convolution(1.13)
Transformée de Fourier : calculons TF[(x*y)(t)] :

Calcul

Ou :
Calcul
On écrit Petite astuce de... calcul... et on obtient, en regroupant :
Encore un calcul
Dans l'intégrale centrale, on effectue le changement de variable Changement de variable ; il vient alors :
Devinez quoi? Des calculs!
On peut ensuite séparer les variables, et on obtient :
Cest presque fini...
Et donc :
Et voilà! TF[(x*y)(t)]=X(nu).Y(nu)(1.14)
Par symétrie dans les relations 1.3 et 1.4, on obtient de même :
TF[(x.y)(t]=X(nu)*Y(nu)(1.15)
La transformée de Fourier de la convolution de deux signaux est le produit de leurs transformées de Fourier, et la transformée de Fourier inverse d'une convolution de deux TF est le produit des deux transformées de Fourier inverses.
Retour en haut de la page
Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).		 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
URL de cette page :
http://www.gchagnon.fr/cours/courlong/1_2_2_6.html