Retour à l'accueil principal

Représentation complexe

 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
Accueil

Régime sinusoïdal, ou harmonique
Définitions
Puissance en régime sinusoïdal
courantReprésentation complexe d'un signal harmonique
Impédances

Table des matières
Index
On considère un signal harmonique x()=x0cos(omega t). On définit alors sa représentation complexe xtilde sous la forme :

xtilde(t)=x0exp(jomega t)

On identifiera par la suite x et xtilde, et on écrira donc souvent par abus de notation x(t)=x0exp(jomega t) . On verra plus tard que l'utilisation de la représentation complexe permet de simplifier les calculs. Pour repasser ensuite dans le domaine réel, il suffit de prendre la partie imaginaire(1) du résultat des calculs(2) : x(t)=I[(xtilde(t)]
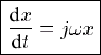
Dérivation : A partir de la forme complexe, il est aisé d'établir une relation entre un signal xtilde(t) et sa dérivée par rapport au temps. En effet, si x(t)=x0exp(jomega t), alors dx/dt=jomega[x0exp(jomega t)], soit :

dx/dt=jomega.x

De même, pour intégrer un signal, il suffit de diviser sa représentation complexe par jomega
Retour en haut de la page
  1. On peut également définir la représentation complexe à partir de 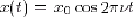x(t)=x0cos(2.pi.nu.t) , auquel cas pour revenir à la représentation réelle du signal il faut prendre la partie réelle.
    Retour au texte
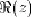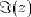  2. Les signes R(z) et I(z) désignent respectivement les parties réelle et imaginaire du nombre complexe z.
    Retour au texte
Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).		 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
URL de cette page :
http://www.gchagnon.fr/cours/courlong/2_3_3.html