Impédances d'entrée/sortie |
Représentation quadripolaire
Introduction
Matrice de transfert
Exemple
Table des matières
Index
On peut essayer de dégager quelques caractéristiques nécessaires pour avoir un "bon" quadripôle.
- En entrée : le quadripôle ne doit pas dégrader les performances de son alimentation. Considérons par exemple un quadripôle, de résistance
d'entrée Re, alimenté par un générateur non idéal, de résistance interne r :
Déterminons Rede manière à réduire les pertes par effet Joule dans le générateur. Ces pertes valent :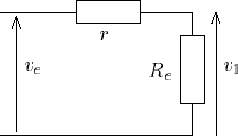
(V désignant la valeur efficace de la tension). Or d'après le théorème du diviseur de tension (cf. paragraphe B.1.1 en annexes) :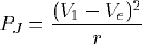
On remarque d'ailleurs sur cette expression que si l'on veut éviter les chutes de tension parasites (autrement dit, être assuré que la tension en entrée du quadripôle est toujours imposée par la force électromotrice du générateur, et ne dépend pas de la résistance interne de celui-ci), il faut que Re soit grande devant r.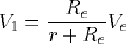
Pour minimiser les pertes par effet Joule dans le générateur, on retrouve la même conclusion : la résistance d'entrée du quadripôle doit être grande devant la résistance du générateur(1).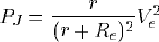
- En sortie : le quadripôle doit présenter la même caractéristique de sortie, quelle que soit la manière dont il est chargé. Considérons
donc un quadripôle de résistance de sortie Rs, chargé par la résistance RL :
La résistance équivalente à ces deux résistances mises en parallèle vaut :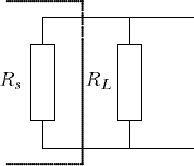
Si on veut que cette résistance diffère peu de RL, il est nécessaire que la résistance de sortie du quadripôle soit petite devant RL.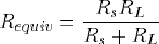
- Adaptation en puissance : les calculs précédents étaient destinés à faciliter l'insertion "transparente" du quadripôle dans un circuit en
cascade. Mais on peut également désirer optimiser le transfert de puissance entre la sortie du quadripôle et sa "charge", c'est-à-dire le composant branché en aval.
Supposons donc que le quadripôle présente une impédance de sortie Zs, un comportement en tension en sortie modélisé par la source
e, et qu'il débite un courant i dans une charge ZL aux bornes de laquelle est mesurée la tension v.
On admet que la puissance dissipée dans ZL par effet Joule est égale à :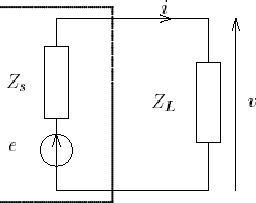
où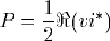
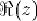 désigne la partie réelle du nombre complexe z, et z* son
conjugué. On a d'après le théorème du diviseur de tension (cf. paragraphe B.1.1) :
désigne la partie réelle du nombre complexe z, et z* son
conjugué. On a d'après le théorème du diviseur de tension (cf. paragraphe B.1.1) :
et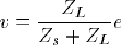
Il vient donc :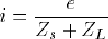
Si on écrit Zs=Rs+jXs, et de même ZL=RL+jXL, on obtient :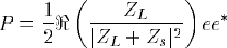
Nous avons vu qu'une impédance complexe pouvait avoir une partie imaginaire positive ou négative. On peut donc faire en sorte que Xs=-XL, autrement dit si le quadripôle doit débiter dans une charge inductive, son impédance de sortie doit être de type capacitif, et réciproquement. Ceci étant établi, il ne reste plus alors qu'à maximiser le facteur RL/(RL+Rs)^2. On montre facilement que cela est réalisé quand Rs=RL(2).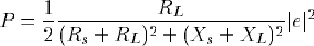
En résumé, pour une adaptation en puissance, il faut que Zs=ZL*. Cette relation est en contradiction avec les résultats précédents, et il est à noter également qu'elle ne peut être rigoureusement vérifiée qu'à une fréquence de fonctionnement fixée. En effet, supposons que la charge vaille 1/jCw. Il faut donc que l'impédance de sortie du quadripôle soit égale à -1/jCw. Cela est possible si on trouve une bobine d'inductance L telle que Lw=1/Cw ; or il n'est possible de réaliser cette égalité qu'en se plaçant à une pulsation déterminée w0, avec L=1/C(w0)^2. Pour une autre pulsation w1, il n'y aura plus adaptation. - Ligne de transmission : se reporter à l'annexe D.
- En fait, on vient d'exprimer fondamentalement la même chose de deux manières différentes. En effet, s'il y a chute de tension, c'est qu'il y a perte
d'énergie quelque part en amont du quadripôle, c'est-à-dire dans la résistance interne du générateur, sous forme d'un dégagement de
chaleur.
Retour au texte - Considérons en effet la fonction
La dérivée de cette fonction vaut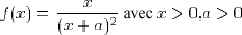
et sa dérivée seconde :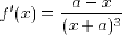
La dérivée s'annule en x=a et comme en ce point la dérivée seconde est négative, il s'agit d'un maximum local.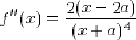
Retour au texte
| Copyright 2000-2010 G. Chagnon Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française). |
http://www.gchagnon.fr/cours/courlong/4_1_4.html