Retour à l'accueil principal
Un exemple d'intérêt du bouclage
 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
Accueil

Généralités
Introduction
Conventions
courantUn exemple d'intérêt du bouclage

Table des matières
Index
Considérons un cas simple d'amplification, tel que la sortie s suive précisément les variations de l'entrée e à un facteur de proportionnalité près. On dit que s est asservie à e. Soit S un système d'amplification de gain K, à l'entrée duquel est injecté le signal e, et à la sortie duquel est mesuré le signal s :

Boite noire, entree e, sortie s

On a donc s=K.e. Supposons que l'on ne connaisse le gain K qu'à 10% près : deltaK/K=0,1. Il est immédiat alors que s ne peut être déterminé qu'à 10% près également : deltas/s=0,1. L'idée à l'origine du concept de contreréaction est de comparer s et e. On construit donc le signal différence entre e et s : epsilon=e-s...

Schema general de la contrereaction

On rappelle que l'opérateur à l'entrée du système est un "soustracteur" et réalise l'opération e-s. On a alors les relations suivantes :

e=epsilon-s et s=K.epsilon

On en déduit :

s=K.e/(1+K)

Si on veut que s suive e avec une erreur la plus faible possible, il faut que K>>1.
Calculons dans ces nouvelles conditions l'influence d'une imprécision portant sur la valeur de K, sur la détermination de s :

deltas/s=(...)=(deltaK/K).[1/(1+K)]

Pour K suffisamment grand, on voit donc que l'incertitude sur s diminue d'un facteur 1/K. Par exemple, avec toujours deltaK/K=0,1 et K=100, on obtient 0,1% seulement.
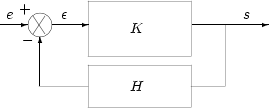
En règle générale cependant, s et e n'ont aucune raison d'être de même nature physique (par exemple, il peut s'agir d'une tension et d'un courant). Il est nécessaire alors d'introduire un capteur de gain H :

Schema general de la contrereaction avec gain H dans la boucle

Cet avantage des systèmes bouclés n'est pas le seul. L'idée à l'origine de leur introduction est qu'il est plus facile d'"asservir" un signal à un autre quand on peut les comparer.
Retour en haut de la page
Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).		 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
URL de cette page :
http://www.gchagnon.fr/cours/courlong/4_2_1_3.html