Retour à l'accueil principal
Exemple
 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
Accueil

Tables de Karnaugh
Principe
Code binaire réfléchi
courantExemple

Table des matières
Index
Pour un système à 4 bits a3a2a1a0, on crée le bit s défini par :

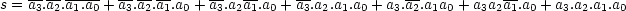
s=non(a3).non(a2).non(a1).non(a0)+non(a3).non(a2).non(a1).a0+non(a3).a2.non(a1).a0+non(a3).a2.a1.a0+a3.non(a2).a1a0+a3.a2.non(a1).a0+a3.a2.a1.a0

Ce bit est défini comme un OU logique sur 7 termes (appelés mintermes). La table de Karnaugh définissant s est la suivante :

bits a1 0 0 1 1
a0 0 1 1
 0
a3 a2    
0 0   1 1 0 0
0 1 0 1 1 0
1 1 0 1 1 0
1 0 0 0 1 0

On peut alors rassembler :

  • les 1 qui se trouvent en haut à gauche du tableau peuvent être rassemblés dans le minterme a3.a2.a1 ;
  • les 1 du milieu du tableau peuvent être rassemblés en a2a0 ;
  • le 1 du bas du tableau s'exprime directement en a3.a2.a1.a0, ou bien peut être rassemblé avec le 1 au-dessus de lui en a3.a1.a0.

Et donc s=a3.a2.a1+a2.a0+a3.a2.a1.a0. Avec un peu d'habitude, les simplifications de ce genre se font beaucoup plus rapidement qu'en partant de l'expression initiale de s.

Retour en haut de la page
Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).		 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
URL de cette page :
  http://www.gchagnon.fr/cours/courlong/5_2_2_3.html