Définitions |
Généralités
Introduction
Table des matières
Index
- Transformée de Fourier : soit un signal x(t) à temps continu, tel que
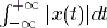 converge(1). On définit alors la transformée de Fourier de x, notée
converge(1). On définit alors la transformée de Fourier de x, notée 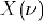 ou (abusivement : cf. plus loin) TF[x(t)], par :
ou (abusivement : cf. plus loin) TF[x(t)], par :
où j est tel que j2=-1(2). La transformée de Fourier permet de mesurer le "contenu fréquentiel" d'un signal, à savoir la manière dont on peut le décomposer en une somme de sinusoïdes de fréquences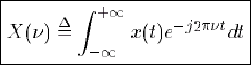 (1.3)
(1.3) .
. - Transformée de Fourier inverse : si de plus x est à énergie finie(3),
cette relation est inversible en
L'opération correspondante est appelée transformation de Fourier inverse : elle permet de revenir au signal temporel x à partir de son contenu fréquentiel.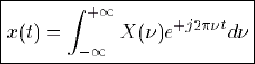 (1.4)
(1.4)
Ces deux définitions permettent de disposer de deux manières de définir complètement un signal qui satisfait aux conditions d'inversibilité de la transformée de Fourier. On peut le définir :
- soit par sa représentation temporelle ;
- soit par sa représentation fréquentielle.
- Spectre : on appelle spectre de x le module de la transformée de Fourier de x :
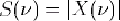
- On dit alors que "
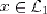 ", ou que x est d'"intégrale absolument convergente".
", ou que x est d'"intégrale absolument convergente".
Retour au texte - On utilise la lettre j et non i comme en mathématiques pour désigner la racine carrée "classique" de -1, pour éviter la confusion avec
le courant i en électricité.
Retour au texte - Rappel :
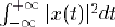 converge.
converge.
Retour au texte
| Copyright 2000-2010 G. Chagnon Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française). |
http://www.gchagnon.fr/cours/courlong/1_2_1_2.html