Cours de génie électrique - Généralités - Spectre et fonction de transfert

Accueil

Spectre d'un signal
Introduction
Signaux multipérioques et apériodiques

Table des matières
Index

Spectre d'un signal multipériodique :il existe des signaux périodiques dont le contenu fréquentiel est infini. Par exemple, le signal carré c(t) suivant...
... présente ce que l'on appelle un "spectre de raies : on montre qu'il peut s'écrire sous la forme⁽¹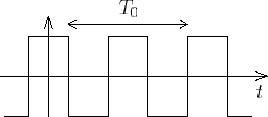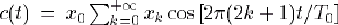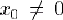⁾ , , avec x_k=x₀/(2k+1). Son spectre présente donc de l'énergie aux fréquences du type f_k=(2k+1)/T₀, avec k entier naturel :
Spectre d'un signal apériodique : comme son nom l'indique, un tel signal n'a pas un nombre "dénombrable"⁽²⁾ de fréquences, mais une infinité. Le spectre d'un tel signal n'est pas un spectre de raies, mais présente des parties continues, par exemple :
On peut considérer qu'il s'agit de la juxtaposition d'un nombre infini d'impulsions de Dirac. On appelle support fréquentiel d'un signal l'intervalle de fréquences entre lesquelles son spectre présente de l'énergie.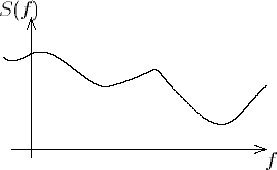

Il est décomposable en série de Fourier. Mathématiquement en fait, il faut de plus qu'un tel signal soit continu, ce qui n'a pas été supposé ; néanmoins, tous les signaux "physiques" en électricité sont continus.
Retour au texte
Que l'on peut compter...
Retour au texte

URL de cette page :
http://www.gchagnon.fr/cours/courlong/2_4_1_2.html