Accueil
Spectre d'un signal
 Introduction Introduction
Signaux multipériodiques et apériodiques
Table des matières
Index |
Nous avons déjà défini ce qu'était un signal "harmonique", ou monochromatique, dans le paragraphe 2.3. Un tel signal ne
présente qu'une unique fréquence. Mais on peut imaginer un signal présentant deux, trois voire une centaine de fréquences différentes. On pourrait
représenter ce signal par son évolution temporelle ; il existe néanmoins une autre manière de le représenter, en mettant en évidence son contenu
fréquentiel. Pour introduire cette nouvelle représentation, nous allons pour un temps revenir à un signal monochromatique, de la forme 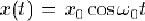 . On peut également écrire, en utilisant une formule d'Euler . On peut également écrire, en utilisant une formule d'Euler
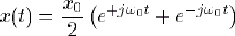
Cette dernière formulation met en évidence le fait que x(t) peut s'écrire comme la somme de deux exponentielles complexes, associées aux pulsations 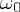 et - et -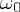 . On
représente ces deux composantes sur un axe gradué en pulsations, ou, mieux, en fréquences, par deux "flèches"(1)
affectées de leurs poids respectifs (en l'occurrence, les deux composantes ont un poids égal à x0/2) : . On
représente ces deux composantes sur un axe gradué en pulsations, ou, mieux, en fréquences, par deux "flèches"(1)
affectées de leurs poids respectifs (en l'occurrence, les deux composantes ont un poids égal à x0/2) :
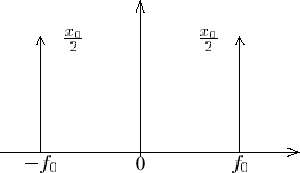
Cette représentation est la représentation fréquentielle du signal, et la fonction X(f) correspondante, ici limitée à deux pics à
±f0, est sa "transformée de Fourier". Le module de X(f), noté Sx(f)=|X(f)|, est le spectre du
signal.
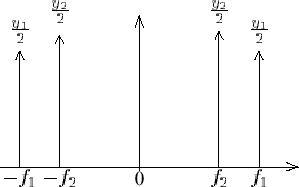
Lorsque l'on a un signal présentant deux fréquences, comme par exemple 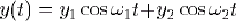 , on obtient facilement de même : , on obtient facilement de même :
Un problème (qui n'en est bien sûr pas un...) semble se poser pour un signal de la forme z(t)=z1cosw1t+z2sinw2t.
Revenons à la décomposition que nous avons déjà utilisée :
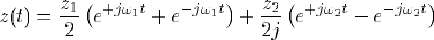
Cette fois-ci, il apparaît que les "poids" des impulsions de Dirac sont des nombres complexes : pour ±f1 il s'agit de z1/2, pour
-f2 de (z2/2).e+j.pi/2 et pour +f2 de (z2/2).e-j.pi/2. Par conséquent, le spectre de z(t) est
rigoureusement égal à celui de y(t), bien que ces deux signaux ne soient pas égaux. En effet, seules les phases de leurs transformées de Fourier
diffèrent, et elles n'apparaissent pas dans le spectre.
URL de cette page :
http://www.gchagnon.fr/cours/courlong/2_4_1_1.html |
![]()


![]()