Définition |
      |
Diagramme de Bode
DéfinitionExemple
Les types de filtre
Table des matières
Index
Partons d'une fonction de transfert en régime harmonique, H(j
), liant deux tensions (1). Comment représenter cette fonction de la
fréquence ? Pour des raisons de commodité, on est
amené à écarter toute représentation
tridimensionnelle (par exemple, en x la fréquence, en y la
partie réelle et en z la partie imaginaire de la fonction). Par
ailleurs, on est plus intéressé par la manière dont le
filtre amplifie le signal à une fréquence donnée,
et de combien il le déphase, plutôt que par la partie
réelle et la partie imaginaire de la fonction de transfert, dont la
signification physique pour un signal quelconque est moins évidente. On
est donc amené à décrire la fonction de transfert sous la
forme de deux diagrammes :
- un diagramme présentant son module en fonction de la fréquence ;
- un deuxième diagramme présentant sa phase.
GdB 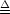 20
log|H(j )| |
Remarque : On peut également introduire la notion d'une fonction de transfert liant deux puissances, HP(j
)=Ps/Pe. Comme la
puissance est proportionnelle au carré de la tension, cette fonction de
transfert est proportionnelle à H(j)2, et on
définit alors le gain en puissance en décibels par
GdB =10 log|H (j)|.
 |
- cf. le paragraphe
1.3.3.
Retour au texte
| Copyright 2000-2010 G. Chagnon Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française). |
|
http://www.gchagnon.fr/cours/courlong/4_3_1_1.html