Fonction de transfert |
Notion de filtre linéaire
Linéarité
Invariance
Table des matières
Index
Soit S un système linéaire invariant, et h sa réponse impulsionnelle. Appliquons à l'entrée de S le signal x(t)=x0est, avec
La fonction de transfert en régime harmonique est la transformée de Fourier de la réponse impulsionnelle, soit :
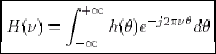 (1.28) (1.28) |
Fonction de transfert et représentation complexe : On a démontré que pour un système linéaire invariant S, de fonction de transfert H(s) dans le cas où l'entrée était de la forme x(t)=x0est, on avait la relation suivante entre l'entrée x et la sortie y : y(t)=H(s)x(t). Lorsque l'on utilise la représentation complexe, en écrivant
| Copyright 2000-2010 G. Chagnon Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française). |
http://www.gchagnon.fr/cours/courlong/1_3_3.html