Retour à l'accueil principal
Théorème de Friiss
 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
Accueil

Facteur de bruit
Définition
Température de bruit
Facteur de bruit d'un quadripôle passif
courantThéorème de Friiss

Table des matières
Index
Considérons par exemple une chaîne de trois quadripôles en cascade, chacun d'eux étant caractérisé par sa température de bruit et son gain en puissance. Ces quadripôles sont supposés adaptés en puissance en entrée et en sortie (cf. paragraphe sur les impédances d'entrée/sortie) :

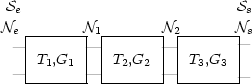
Trois quadripoles en cascade

Hypothèses et définitions : chaque quadripôle possède une température de bruit Ti, une température de bruit ramenée en entrée Tri , un gain en puissance Gi. La puissance totale du bruit en sortie du premier quadripôle est N1, en sortie du deuxième N2 et en sortie de la chaîne Ns. NQi désigne le bruit produit par le quadripôle i. La puissance de signal vaut Se en entrée, et Ss en sortie. La bande passante de travail est B. Les quadripôles sont adaptés en puissance (1). T0 est la température de référence d'une source de bruit étalon, Ts la température associée au bruit total mesuré en sortie. On cherche à déterminer le gain en puissance total G et la température de bruit ramenée en entrée Tr du quadripôle équivalent aux trois montés en série.
  1. Il est facile de démontrer que 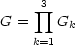G=produit(k=1 a 3)Gk (2).
  2. On a :

    Trois equations sur N1, N2 et N3

    On en déduit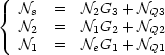

    Ns=NeG1G2G3+G2G3Nq1+G3Nq2+Nq3

    Avec Ne=kBT0,NQ1=kBT1, NQ2=kBT2 et NQ3=kBT3 il vient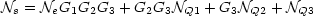

    Ns = kBT0G1G2G3 + kBT1G2G3 + kBT2G3 + kBT3

    Soit

    une formule compliquee

    Calculons le facteur de bruit du quadripôle équivalent :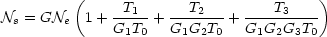

    une formule compliquee

    En identifiant avec la relation définissant le facteur de bruit, on obtient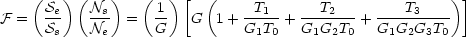

    Tr=Tr1+Tr2/G1+Tr3/(G1G2)

    En résumé, sous réserve d'adaptation en puissance :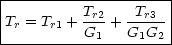
    • Le gain en puissance d'une chaîne de quadripôles est égal au produit des gains en puissance ;
    • La température de bruit ramenée en entrée est égale à

      Tr=somme(i=1...n)[Tri/Produit(j=0...i-1)Gj]

      avec la convention G0=1.
      On remarque qu'une température joue un plus grand rôle que les autres : celle du premier quadripôle. Une conséquence remarquable est que si on veut diminuer le bruit à la sortie d'une chaîne de quadripôles, il est nécessaire de placer en tête de la chaîne un quadripôle de faible température de bruit, et de surcroît amplificateur, pour diminuer encore plus l'influence des bruits dûs aux autres quadripôles.
Retour en haut de la page
  1. cf. paragraphe 4.1.4.
    Retour au texte
  2. Le symbole 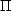pi majuscule indique le produit. Ici, G=G1G2G3.
    Retour au texte
Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).		 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
URL de cette page :
  http://www.gchagnon.fr/cours/courlong/4_4_4_4.html