Retour à l'accueil principal
Associations de résistors
 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
Accueil

Dipôles électriques
L'effet résistif
Loi d'Ohm
Aspect énergétique
courantAssociations de résistors

Table des matières
Index
Considérons deux résistances R1 et R2. On peut les associer de deux manières : soit elles sont parcourues par le même courant (association en série), soit elles sont soumises à la même différence de potentiel (association en parallèle). On cherche dans chaque cas la résistance R équivalente à l'ensemble de R1 et R2.
  1. Association en série ; les deux résistances sont associées ainsi :
    Association en série
    La loi des mailles (paragraphe 2.1.3.2) nous permet d'écrire U=U1+U2. Or on a aussi U1=R1i et U2=R2i. Il vient donc U=(R1+R2)i, soit R=R1+R2 :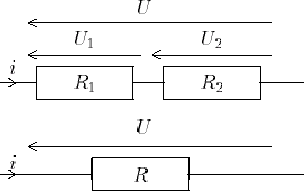
    La résistance équivalente à deux résistances mises en série est égale à la somme des résistances.
  2. Association en parallèle ; les deux résistances sont associées ainsi :
    Association en parallèle
    On note leurs conductances respectives G1, G2 et la conductance équivalente G. La loi des noeuds (paragraphe 2.1.3.1) nous permet d'écrire i=i1+i2. Or on a aussi i1=G1U et i2=G2U. Il vient donc i=(G1+G2)U, soit G=G1+G2 :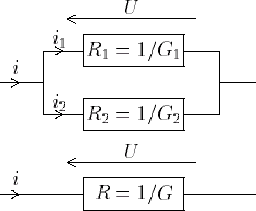
    La conductance équivalente à deux conductances mises en parallèle est égale à la somme des conductances.
    Autrement dit, l'inverse de la résistance équivalente est égale à la somme des inverses des résistances.
Retour en haut de la page
Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).		 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
URL de cette page :
http://www.gchagnon.fr/cours/courlong/2_2_1_4.html