Accueil
Représentation de Fourier des signaux d'énergie infinie
 Impulsion de Dirac Impulsion de Dirac
Spectre des signaux périodiques
Cas particulier : peigne de Dirac
Table des matières
Index |
Définition : on introduit 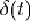 , noté impulsion de Dirac(1), défini par sa transformée de Fourier, tel que :
où 1 désigne la fonction uniformément égale à 1 sur , noté impulsion de Dirac(1), défini par sa transformée de Fourier, tel que :
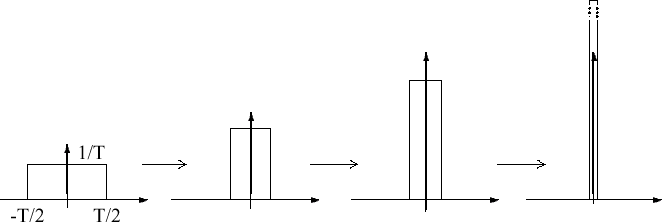
où 1 désigne la fonction uniformément égale à 1 sur 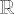 . Plus "physiquement", . Plus "physiquement", 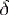 est la limite quand est la limite quand 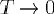 du signal suivant :
On représente graphiquement cette impulsion ainsi :
Propriétés : soit x un signal à temps continu, d'énergie finie. du signal suivant :
On représente graphiquement cette impulsion ainsi :
Propriétés : soit x un signal à temps continu, d'énergie finie.
- Calculons
![TF[x delta]](images/1/1_2/image61.gif) : il s'agit de la transformée de Fourier d'un produit, donc en appliquant la formule 1.15, le résultat est la convolution des deux transformées de Fourier :
On écrit : il s'agit de la transformée de Fourier d'un produit, donc en appliquant la formule 1.15, le résultat est la convolution des deux transformées de Fourier :
On écrit 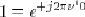 , et on obtient :
Or le membre de droite n'est autre que la valeur prise par x(t) en t=0 (cf. définition 1.4 de la transformée de Fourier
inverse). Il vient donc :
En particulier, pour , et on obtient :
Or le membre de droite n'est autre que la valeur prise par x(t) en t=0 (cf. définition 1.4 de la transformée de Fourier
inverse). Il vient donc :
En particulier, pour 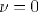 , on obtient facilement :
En généralisant, on obtient également facilement par un changement de variable : , on obtient facilement :
En généralisant, on obtient également facilement par un changement de variable :
- Calculons également
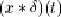 :
L'impulsion de Dirac est donc l'élément neutre de la convolution. :
L'impulsion de Dirac est donc l'élément neutre de la convolution.
- La définition 1.16 se traduit par :
mais également par symétrie entre les relations 1.3 et 1.4, par :
- Impulsion de Dirac et échelon de Heaviside. L'échelon de Heaviside est défini par :
Soient a et b deux réels non nuls, b>a. Calculons
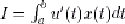 :
en utilisant une intégration par parties (cf. note 1 du paragraphe 1.2.2.3). Trois cas se présentent alors : :
en utilisant une intégration par parties (cf. note 1 du paragraphe 1.2.2.3). Trois cas se présentent alors :
- a>0 et b>0 : alors u(b)=u(a)=1, et
I=u(b)x(b)-u(a)x(a)-[x(b)-x(a)]=0
- a<0 et b<0 : alors u(b)=u(a)=0, et
- a<0 et b<0 : alors u(b)=1 et u(a)=0, et
- Cette relation devant être vérifiée quels que soient a et b, on obtient :
En comparant avec la relation 1.18, et ces égalités devant être vérifiées quel que soit le signal x, il vient donc que
La dérivée de l'échelon de Heaviside est l'impulsion de Dirac.
 |
URL de cette page :
http://www.gchagnon.fr/cours/courlong/1_2_3_1.html |
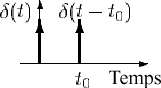
![TF[x delta]](images/1/1_2/image61.gif) : il s'agit de la transformée de Fourier d'un produit, donc en appliquant la formule 1.15, le résultat est la convolution des deux transformées de Fourier :
: il s'agit de la transformée de Fourier d'un produit, donc en appliquant la formule 1.15, le résultat est la convolution des deux transformées de Fourier :
![TF[x(t)delta(t)]](images/1/1_2/image62.gif)
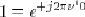 , et on obtient :
, et on obtient :
![TF[x(t)delta(t)]](images/1/1_2/image64.gif)
![TF[x(t)delta(t)]=x(0)](images/1/1_2/image65.gif) (1.17)
(1.17)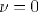 , on obtient facilement :
, on obtient facilement :
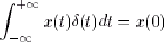 (1.18)
(1.18)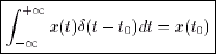 (1.19)
(1.19)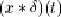 :
:
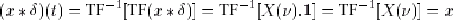
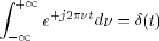
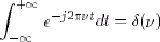 (1.20)
(1.20)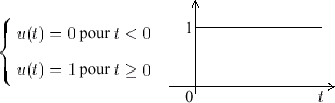
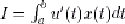 :
:
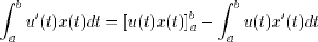
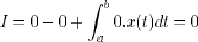
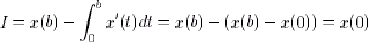
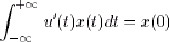
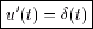 (1.21)
(1.21)