Accueil
Notion de filtre linéaire
Linéarité
 Invariance
Fonction de transfert
Table des matières
Index |
Comme il a été souligné dans le paragraphe précédent, la réponse du système dépend a priori de l'instant où il
est excité. L'invariance est la traduction du fait que l'on désire que cette réponse ne dépende plus de cet instant. Autrement dit, si y(t) est la réponse au
signal x(t), alors le signal 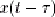 doit entraîner la réponse  .
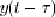Soit donc le signal x1(t) ; son image par le sytème S est le signal y1(t). On considère le signal 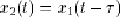 (il s'agit du signal x1 retardé du temps  ) ; son image est le
signal y2(t). On cherche à avoir 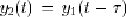 . Traduisons cette égalité en utilisant la
relation 1.26 :
Soit :
On effectue dans la première intégrale le changement de variable 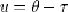 ; il vient alors :
Cette égalité devant être vérifiée quel que soit le signal x1, on a donc nécessairement, quels que soients t, , u :
En particulier, pour u=0, on obtient :
La fonction de deux variables 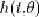 peut donc se mettre sous la forme d'une fonction de la différence
de ces deux variables. Par la suite, pour un système linéaire invariant, nous écrirons donc plus simplement 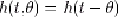 . En remplaçant dans l'équation 1.26, on obtient :
Soit, plus simplement, en comparant avec la relation 1.12 :
La réponse d'un système linéaire invariant à une entrée quelconque est la convolution de cette entrée par la réponse impulsionnelle du
système.
URL de cette page :
http://www.gchagnon.fr/cours/courlong/1_3_2.html |
(1.27)
