Cours de génie électrique - Systèmes analogiques - Bruit dans les composants - Densité spectrale de puissance

Retour à l'accueil principal

Densité spectrale de puissance

Accueil

Bruit dans les composants
Densité spectrale de puissance
Les types de bruit
Bruit dans un dipôle
Facteur de bruit

Table des matières
Index

On rappelle que le spectre⁽¹⁾ d'un signal est le module de sa transformée de Fourier. On définit la densité spectrale de puissance comme étant le carré du module de la transformée de Fourier. Ainsi, si x est un signal et X sa transformée de Fourier, sa densité spectrale de puissance vaut

D_x = |X()|²

Il existe une autre expression de la densité spectrale de puissance. Introduisons la notion de fonction d'autocorrélation d'un signal x à temps continu :

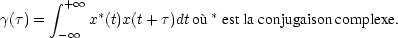
Prise au point

, cette fonction mesure en quelque sorte la manière dont les structures que l'on peut voir dans un signal se répètent sur des échelles de temps de

. Calculons sa transformée de Fourier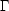

(

) :

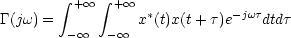
Cette expression peut se mettre sous la forme :

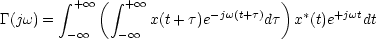
On effectue dans l'intégrale le changement de variable u=t+

et il vient :

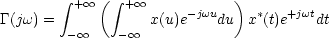
Soit encore :

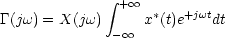
On effectue le changement de variable u=-t et on obtient :

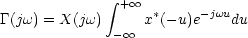
On reconnaît dans le deuxième terme la transformée de Fourier de x*(-t). Or d'après la propriété 1.11, la transformée de Fourier de x* vaut X*(-

), et d'après 1.10, la transformée de Fourier de x(-t) vaut X(-

). Le deuxième terme vaut donc X*(j

), donc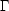

(j

) =X(j

) X*(j

) =|X(j

)|² : la densité spectrale de puissance est aussi la transformée de Fourier de l'autocorrélation.

cf. le paragraphe 1.2.1.2
Retour au texte

Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).

URL de cette page :
http://www.gchagnon.fr/cours/courlong/4_4_1.html