Cours de génie électrique - Systèmes analogiques - Bruit dans les composants - Les types de bruit

Bruit thermique

Accueil

Les types de bruit
Bruit thermique
Bruit de grenaille
Bruit en 1/f
Bruit en créneaux

Table des matières
Index

Egalement nommé bruit de résistance, ou bruit Johnson, du nom du physicien Johnson qui l'a mis en évidence en 1927.
L'étude théorique en a été faite en 1928 par Nyquist. Quand un corps est porté à une certaine température, les noyaux atomiques mais surtout les électrons qui le composent (en raison de leur plus faible masse) sont agités, et dotés d'une vitesse en moyenne nulle (ils ne vont en moyenne dans aucune direction particulière), mais dont la moyenne quadratique (c'est-à-dire la racine carrée de la moyenne des carrés des vitesses) est proportionnelle au produit de la température, exprimée en degrés Kelvin, et d'une constante k, appelée constante de Boltzmann, qui vaut k= 1.38.10-23J/K :
Pour une résistance R portée à la température T, la densité spectrale de puissance du bruit vaut D_R=2kRT⁽¹⁾. Elle s'exprime en Volts au carré par Hertz (V²/Hz). Ce bruit est dit blanc, par analogie avec la lumière visible, car toutes les fréquences sont également représentées dans le spectre. Cela n'est pas rigoureusement exact (l'énergie transportée par un tel signal serait infinie), mais cette approximation est tout à fait valable dans les domaines de fréquences où l'on travaille habituellement.
Exemple : circuit RC. Considérons le circuit suivant :

Il est facile de montrer que la fonction de transfert de ce filtre vaut :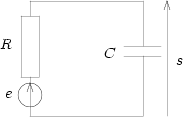

avec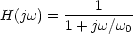 ₀=1/RC. La résistance "bruyante" peut être modélisée comme étant la mise en série d'une résistance parfaite, non bruyante, et d'une source e_b délivrant une tension dont la densité spectrale de puissance est celle du bruit. Cette source de tension est filtrée de la même manière par le circuit. La composante bruitée s_b de la sortie vaut donc à la fréquence

Calculons la transformée de Fourier ; il vient

Prenons-en le module au carré ; le terme de gauche devient la densité spectrale de puissance du bruit en sortie, et la Transformée de Fourier de droite la densité spectrale de puissance de l'entrée bruitée, donc du bruit thermique dû à la résistance :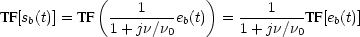

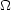Application numérique : dans notre cas, R=10k , T=300K, C=1,6nF. La fréquence de coupure vaut alors ₀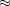10kHz. La puissance totale transportée par le bruit vaut 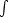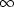_-⁺ Ds()d, soit 2kRT₀.
En règle générale, on dira en fait que la puissance de bruit totale vaut en première approximation la densité spectrale de puissance de bruit en entrée, multipliée par la bande passante du système (ici ₀). Avec les valeurs numériques choisies, on obtient donc environ 2kRT₀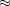10^-12 V². Le bruit uniquement dû à cette résistance est donc équivalent à une source de tension moyenne d'environ 1V.

On peut aussi trouver D_R=4kRT. Tout est une question de définition de la transformée de Fourier. Nous utilisons dans ce cours la définition dans laquelle les bornes d'intégration de l'intégrale généralisée son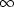t - et +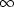 (cf paragraphe 1.2.1.2). Cette définition est dite bilatérale. On peut également définir une autre TF, où le domaine d'intégration s'étend de 0 à +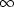 seulement. Cette TF est dite monolatérale, mais ne vérifie pas tout à fait les mêmes propriétés.
Retour au texte

URL de cette page :
http://www.gchagnon.fr/cours/courlong/4_4_2_1.html