Spectre de signaux périodiques |
Représentation de Fourier des signaux dénergie infinie
Impulsion de Dirac
Cas particulier : peigne de Dirac
Table des matières
Index
Soit x(t) un signal à temps continu, de période T. On admet que x(t) est "développable en série de Fourier" sous la forme :
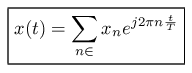 (1.22) (1.22) |
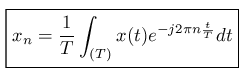 (1.23) (1.23) |
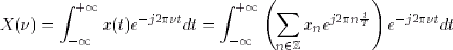 |
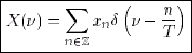 (1.24) (1.24) |
On considère le signal T-périodique x(t) tel que :
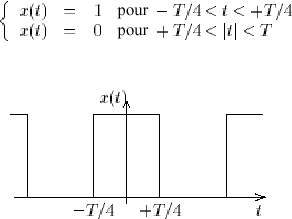 |
- Mathématiquement, cela nécessite la convergence uniforme de la série. Dans la "réalité", les échantillons xn
étant nécessairement nuls à partir et en-dessous d'un certain rang, cette condition est toujours vérifiée.
Retour au texte
| Copyright 2000-2010 G. Chagnon Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française). |
http://www.gchagnon.fr/cours/courlong/1_2_3_2.html