Retour à l'accueil principal
Dérivation
 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
Accueil

Propriétés
Linéarité
Décalage en temps/fréquence
courantDérivation
Dilatation en temps/fréquence
Conjugaison complexe
Convolution
Table des matières
Index
On note x'(t)=dx/dt. Alors :
Application de la formule de la TF
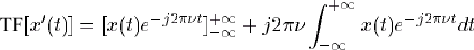On effectue une intégration par parties(1) en intégrant x'(t) et en dérivant l'exponentielle complexe. On obtient alors :
intégration par parties
Comme x est, physiquement, nécessairement nul à +/- linfini(2), et que l'exponentielle complexe y reste bornée, le premier terme de la somme devient nul et donc :
TF de la dérivée(1.8)
Retour en haut de la page
  1. Rappel sur l'intégration par parties : Soient f et g deux fonctions dérivables et définies sur l'intervalle [a,b], dont les dérivées sont continues sur ]a,b[. Alors :
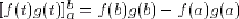    intégration par parties
    avec intégration par parties.
    Retour au texte
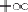  2. Un signal observé est toujours nul en -infini car il n'était alors pas encore observé, et nul en +infini car il ne l'est plus.
    Retour au texte
Copyright 2000-2010 G. Chagnon
Copyright (c) 2001-2010 Gilles Chagnon. Ce document est publié selon les termes de la GNU Free Documentation License (version française).		 Revenir au niveau supérieur Revenir au niveau supérieur Revenir à la section précédente Aller à la section suivante Index Table des matières
URL de cette page :
http://www.gchagnon.fr/cours/courlong/1_2_2_3.html